1520. Нечетные делители
Пусть f(n) – наибольший
нечетный делитель натурального числа n.
Для заданного натурального числа n
вычислите значение суммы:
f(1) + f(2) + ... + f(n)
Вход. Каждая строка содержит одно натуральное число n (n
≤ 109).
Выход. Для каждого
значения n выведите в отдельной
строке значение суммы f(1) + f(2) + ... + f(n).
|
Пример
входа |
Пример
выхода |
|
7 1 777 |
21 1 201537 |
РЕШЕНИЕ
рекурсия
Анализ алгоритма
Если число n
нечетное, то f(n) = n.
Если число n
четное, то f(n) = f(n / 2).
Пусть
g(n) = f(1) + f(2)
+ ... + f(n)
Рассмотрим разбиение
множества натуральных чисел от 1 до n на два подмножества:
·
ODD – множество нечетных чисел,
·
EVEN – множество четных чисел.
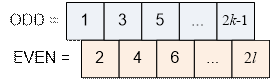
Среди
натуральных чисел от 1 до n имеется ровно:
·
k = 
нечетных
·
l = 
четных чисел
Тогда:
f(1) + f(3) + f(5)
+ ... + f(2k – 1) =
1 + 3 + 5 + … + (2k
– 1) =
= k2
В то же время:
f(2) + f(4) + f(6)
+ ... + f(2l) =
f(1) + f(2) + f(3)
+ ... + f(l) =
g(l) = 
Для окончания
рекурсии положим g(0) = 0. Таким образом:
Пример
Рассмотрим
первый тест, в котором n = 7.
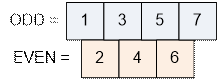
Среди
натуральных чисел от 1 до 7 имеется в точности:
·
k = 
= 4 нечетных числа;
·
l = 
= 3 четных числа.
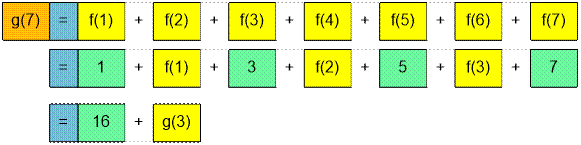
g(7) = 
+ 
= 16 + g(3) =
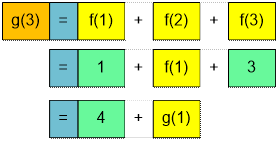
16 + 
+ 
= 16 + 4 + g(1) = 16 +
4 + 1 = 21
Реализация алгоритма
Реализуем функцию g.
long long
g(long long n)
{
long long k = (n + 1) / 2;
if (n == 0) return 0;
return k * k
+ g(n / 2);
}
Основная часть программы. Читаем входное
значение n и выводим g(n).
while(scanf("%lld",&n)
== 1)
printf("%lld\n",g(n));
Java реализация
import java.util.*;
public class Main
{
static long g(long n)
{
long k = (n + 1) / 2;
if (n == 0) return 0;
return k * k + g(n / 2);
}
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
while(con.hasNext())
{
long n = con.nextLong();
System.out.println(g(n));
}
}
}
Python реализация
import sys
def g(n):
if
n == 0:
return
0
k = (n + 1) // 2
return
k * k + g(n // 2)
for line in
sys.stdin:
n = int(line)
print(g(n))